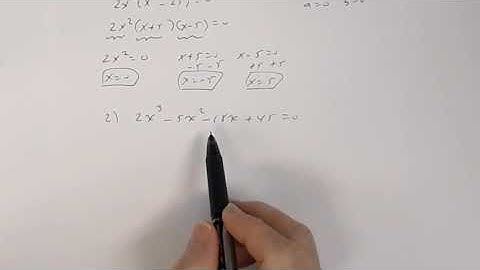Upgrade to remove ads Show Only $35.99/year
Terms in this set (5)(-4, -1) Solve the system by graphing: y = -1/2x - 3 (-4, 4) Solve the system by graphing: x = -4 (-3, 3) Solve the system by graphing: y = 3 No Solution Solve the system by graphing: x - 3y = -12 Infinitely Many Solutions Solve the system by graphing: -8x - 4y = -16 Sets with similar termsSystem of Equations15 terms suerossello Systems of Equations Substitution Easy12 terms Kathleen_McCullough5 Systems of Equations, Systems of Equatio…12 terms Kimberly_Whitehead Linear Equation Review25 terms d52sstriTEACHER Other sets by this creatorSolving Systems of Linear Equations using Eliminat…5 terms MrsLakes-Williams Solving Systems of Linear Equations using Substitu…5 terms MrsLakes-Williams Verified questions
LINEAR ALGEBRA Create a symmetric matrix by substituting appropriate numbers for the x's. (b) [1 x x x, 3 1 x x, 7 -8 0 x, 2 -3 9 0] Verified answer
LINEAR ALGEBRA (a) for what values of h is $\mathbf{v}_{3}$ is Span $\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\}$, and (b) for what values of h is $\left\{\mathbf{v}_{1}, \mathbf{v}_{2}, \mathbf{v}_{3}\right\}$ linearly dependent? Justify each answer. $$ \mathbf{v}_{1}=\left[ \begin{array}{r}{1} \\ {-3} \\ {2}\end{array}\right], \mathbf{v}_{2}=\left[ \begin{array}{r}{-3} \\ {9} \\ {-6}\end{array}\right], \mathbf{v}_{3}=\left[ \begin{array}{r}{5} \\ {-7} \\ {h}\end{array}\right] $$ Verified answer LINEAR ALGEBRA Make a change of variable, x=Py, that transforms the quadratic form $x_{1}^{2}+10 x_{1} x_{2}+x_{2}^{2}$ into a quadratic form with no cross-product term. Give P and the new quadratic form. Verified answer
LINEAR ALGEBRA In each part, determine whether the matrices are linearly independent or dependent. (a) [1 0, 1 2] [1 2, 2 1] [0 1, 2 1] in M22 Verified answer Recommended textbook solutions
 Calculus, Volume 2: Multi-Variable Calculus and Linear Algebra with Applications to Differential Equations and Probability2nd EditionTom M. Apostol 1,036 solutions
 Elementary Linear Algebra11th EditionHoward Anton 2,914 solutions  Linear Algebra and Its Applications5th EditionDavid C. Lay, Judi J. McDonald, Steven R. Lay 2,028 solutions
 Linear Algebra with Applications5th EditionOtto Bretscher 2,515 solutions Other Quizlet setsGB 370 Unit 375 terms hchamric COMS FINAL, COMS Test 1240 terms AbigailRobles16 Managerial Accounting Chapter 1 Notes26 terms dawsonjack11 Chapter 24- Pre-Test Summary34 terms Emily5234554 Related questionsQUESTION What is Conjunctive Normal Form (CNF)? 8 answers QUESTION What is the equation of tangent? 15 answers QUESTION The determinant of A is the product of the pivots in any echelon form U of A, multiplied by (-1)^r, where r is the number of row interchanges made during row reduction from A to U. 15 answers QUESTION Two planes perpendicular to a third plane are parallel. 15 answers How do you solve a linear system by graphing?To solve a system of linear equations graphically we graph both equations in the same coordinate system. The solution to the system will be in the point where the two lines intersect. The two lines intersect in (-3, -4) which is the solution to this system of equations.
What is the solution to the system of linear equations quizlet?The solution to a system of linear equations is the point at which the lines representing the linear equations intersect. Two lines in the xy-plane CAN INTERSECT ONCE never completely overlapping. 2. If the two lines have the same slope but different y-intercepts, then they are parallel lines and will NEVER INTERSECT.
What is the solution to the system of equations 2x y 7 y 2x 3?Summary: The system of linear equations 2x - y = 7, and y = 2x + 3, has no solution.
How many solutions does this linear system have y 2x 5 8x 4y =Summary: The linear system y = 2x - 5 and -8x - 4y = -20 has only one solution.
|

Related Posts
Advertising
LATEST NEWS
Advertising
Populer
Advertising
About

Copyright © 2024 nguoilontuoi Inc.