Differential equations with boundary value problems solution

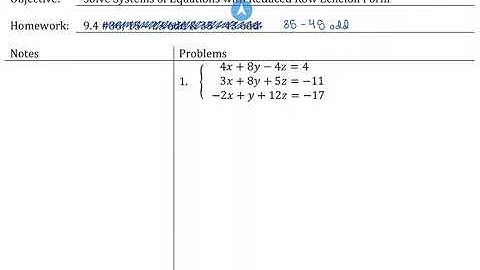
1. Second order; linear 2. Third order; nonlinear because of (dy/dx) 4 3. Fourth order; linear 4. Second order; nonlinear because of cos(r + u) 5. Second order; nonlinear because of (dy/dx) 2 or 1 + (dy/dx) 2 6. Second order; nonlinear because of R 2 7. Third order; linear 8. Second order; nonlinear because of ˙ x 2 9. Writing the differential equation in the form x(dy/dx) + y 2 = 1, we see that it is nonlinear in y because of y 2. However, writing it in the form (y 2 − 1)(dx/dy) + x = 0, we see that it is linear in x. 10. Writing the differential equation in the form u(dv/du) + (1 + u)v = ue u we see that it is linear in v. However, writing it in the form (v + uv − ue u)(du/dv) + u = 0, we see that it is nonlinear in u. 11. From y = e −x/2 we obtain y = − 1 2 e −x/2. Then 2y + y = −e −x/2 + e −x/2 = 0. 12. From y = 6 5 − 6 5 e −20t we obtain dy/dt = 24e −20t , so that dy dt + 20y = 24e −20t + 20 6 5 − 6 5 e −20t = 24. 13. From y = e 3x cos 2x we obtain y = 3e 3x cos 2x − 2e 3x sin 2x and y = 5e 3x cos 2x − 12e 3x sin 2x, so that y − 6y + 13y = 0. 14. From y = − cos x ln(sec x + tan x) we obtain y = −1 + sin x ln(sec x + tan x) and y = tan x + cos x ln(sec x + tan x). Then y + y = tan x. 15. The domain of the function, found by solving x + 2 ≥ 0, is [−2, ∞). From y = 1 + 2(x + 2) −1/2 we have (y − x)y = (y − x)[1 + (2(x + 2) −1/2 ] = y − x + 2(y − x)(x + 2) −1/2 = y − x + 2[x + 4(x + 2) 1/2 − x](x + 2) −1/2 = y − x + 8(x + 2) 1/2 (x + 2) −1/2 = y − x + 8.

Table of Contents Show

How do you solve differential equations with boundary conditions?
What is the solution of the boundary value problem?
What is boundary value problem in differential equations?
How many solutions does a boundary value problem have?

Problems 1.1.1 - 1.3.16

Problems 1.3.17 - 2.2.14

Problems 2.2.15 - 2.4.14

Problems 2.4.15 - 2.6.20

Problems 2.6.21 - 2.9.12

Problems 2.9.13 - 3.1.8

Problems 3.1.9 - 3.2.48

Problems 3.2.49 - 3.4.18

Problems 3.4.19 - 3.5.39

Problems 3.6.1 - 3.8.4

Problems 3.8.5 - 4.2.22

Problems 4.2.23 - 5.1.12

Problems 5.1.13 - 5.3.24

Problems 5.3.25 - 5.5.12

Problems 5.5.13 - 6.1.28

Problems 6.1.29 - 6.3.28

Problems 6.3.29 - 6.6.4

Problems 6.6.5 - 7.2.20

Problems 7.2.21 - 7.5.16

Problems 7.5.17 - 7.8.4

Problems 7.8.5 - 8.1.27

Problems 8.2.1 - 8.5.9

Problems 8.6.1 - 9.3.8

Problems 9.3.9 - 9.6.8

Problems 9.6.9 - 10.2.4

Problems 10.2.5 - 10.4.24

Problems 10.4.25 - 10.7.4

Problems 10.7.5 - 11.2.8

Problems 11.2.9 - 11.6.13

Chapter 1: Introduction
- Section 1.1: Some Basic Mathematical Models; Direction Fields
- Section 1.2: Solutions of Some Differential Equations
- Section 1.3: Classification of Differential Equations
- Section 1.4: Historical Remarks
Chapter 2: First Order Differential Equations
- Section 2.1: Linear Equations; Method of Integrating Factors
- Section 2.2: Separable Equations
- Section 2.3: Modeling with First Order Equations
- Section 2.4: Differences Between Linear and Nonlinear Equations
- Section 2.5: Autonomous Equations and Population Dynamics
- Section 2.6: Exact Equations and Integrating Factors
- Section 2.7: Numerical Approximations: Euler's Method
- Section 2.8: The Existence and Uniqueness Theorem
- Section 2.9: First Order Difference Equations
Chapter 3: Second Order Linear Equations
- Section 3.1: Homogeneous Equations with Constant Coefficients
- Section 3.2: Solutions of Linear Homogeneous Equations; the Wronskian
- Section 3.3: Complex Roots of the Characteristic Equation
- Section 3.4: Repeated Roots; Reduction of Order
- Section 3.5: Nonhomogeneous Equations; Method of Undetermined Coefficients
- Section 3.6: Variation of Parameters
- Section 3.7: Mechanical and Electrical Vibrations
- Section 3.8: Forced Vibrations
Chapter 4: Higher Order Linear Equations
- Section 4.1: General Theory of nth Order Linear Equations
- Section 4.2: Homogeneous Equations with Constant Coefficients
- Section 4.3: The Method of Undetermined Coefficients
- Section 4.4: The Method of Variation of Parameters

Chapter 5: Series Solutions of Second Order Linear Equations
- Section 5.1: Review of Power Series
- Section 5.2: Series Solutions Near an Ordinary Point, Part I
- Section 5.3: Series Solutions Near an Ordinary Point, Part II
- Section 5.4: Euler Equations; Regular Singular Points
- Section 5.5: Series Solutions Near a Regular Singular Point, Part I
- Section 5.6: Series Solutions Near a Regular Singular Point, Part II
- Section 5.7: Bessel's Equation
Chapter 6: The Laplace Transform
- Section 6.1: Definition of the Laplace Transform
- Section 6.2: Solution of Initial Value Problems
- Section 6.3: Step Functions
- Section 6.4: Differential Equations with Discontinuous Forcing Functions
- Section 6.5: Impulse Functions
- Section 6.6: The Convolution Integral
Chapter 7: Systems of First Order Linear Equations
- Section 7.1: Introduction
- Section 7.2: Review of Matrices
- Section 7.3: Systems of Linear Algebraic Equations; Linear Independence, Eigenvalues, Eigenvectors
- Section 7.4: Basic Theory of Systems of First Order Linear Equations
- Section 7.5: Homogeneous Linear Systems with Constant Coefficients
- Section 7.6: Complex Eigenvalues
- Section 7.7: Fundamental Matrices
- Section 7.8: Repeated Eigenvalues
- Section 7.9: Nonhomogeneous Linear Systems
Chapter 8: Numerical Methods
- Section 8.1: The Euler or Tangent Line Method
- Section 8.2: Improvements on the Euler Method
- Section 8.3: The Runge-Kutta Method
- Section 8.4: Multistep Methods
- Section 8.5: Systems of First Order Equations
- Section 8.6: More on Errors; Stability

Chapter 9: Nonlinear Differential Equations and Stability
- Section 9.1: The Phase Plane: Linear Systems
- Section 9.2: Autonomous Systems and Stability
- Section 9.3: Locally Linear Systems
- Section 9.4: Competing Species
- Section 9.5: Predator-Prey Equations
- Section 9.6: Liapunov's Second Method
- Section 9.7: Periodic Solutions and Limit Cycles
- Section 9.8: Chaos and Strange Attractors: The Lorenz Equations
Chapter 10: Partial Differential Equations and Fourier Series
- Section 10.1: Two-Point Boundary Value Problems
- Section 10.2: Fourier Series
- Section 10.3: The Fourier Convergence Theorem
- Section 10.4: Even and Odd Functions
- Section 10.5: Separation of Variables; Heat Conduction in a Rod
- Section 10.6: Other Heat Conduction Problems
- Section 10.7: The Wave Equation: Vibrations of an Elastic String
- Section 10.8: Laplace's Equation
Chapter 11: Boundary Value Problems and Sturm-Liouville Theory
- Section 11.1: The Occurence of Two-Point Boundary Value Problems
- Section 11.2: Sturm-Liouville Boundary Value Problems
- Section 11.3: Nonhomogeneous Boundary Value Problems
- Section 11.4: Singular Sturm-Liouville Problems
- Section 11.5: Further Remarks on the Method of Separation of Variables: A Bessel Series Expansion
- Section 11.6: Series of Orthogonal Functions: Mean Convergence

How do you solve differential equations with boundary conditions?

In the earlier chapters we said that a differential equation was homogeneous if g(x)=0 g ( x ) = 0 for all x . Here we will say that a boundary value problem is homogeneous if in addition to g(x)=0 g ( x ) = 0 we also have y0=0 y 0 = 0 and y1=0 y 1 = 0 (regardless of the boundary conditions we use).

What is the solution of the boundary value problem?

In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions.

What is boundary value problem in differential equations?

A Boundary value problem is a system of ordinary differential equations with solution and derivative values specified at more than one point. Most commonly, the solution and derivatives are specified at just two points (the boundaries) defining a two-point boundary value problem.